Autoregressive Moving Average (ARMA)


Autoregressive (AR)
t보다 이전에 있었던 정보들을 모두 합한 정보로 yt를 설명한다는 의미를 가짐
y에 대해서 p만큼의 과거를 가지고 현재값 예측

Moving Average (MA)
ε: 예측값과 실제값의 차이 (residual 혹은 error 로 불림)
βo: 항상 1 (βo이면 εt는 yt와 항상 동시에 일어남 -> βo를 존재한다고 가정하고 1로 놓는다)
ε에 대해서 q만큼의 과거를 가지고 현재값 예측
αi와 βo를 제외한 βi는 회귀(OLS 등)를 통해 추론
ARMA 조건
시계열 데이터가 Stationary Process(정상성을 가진 데이터)여야 함
=> 정상성을 갖게 하기 위해 차분을 추가 → ARIMA
covariance stationay(공분산 정상성)일 조건

1. 시간에 관계없이 평균이 항상 동일해야 한다. (트렌드 존재하면 안됨)

2. 시간에 따라 공분산이 변하지 않아야 한다.
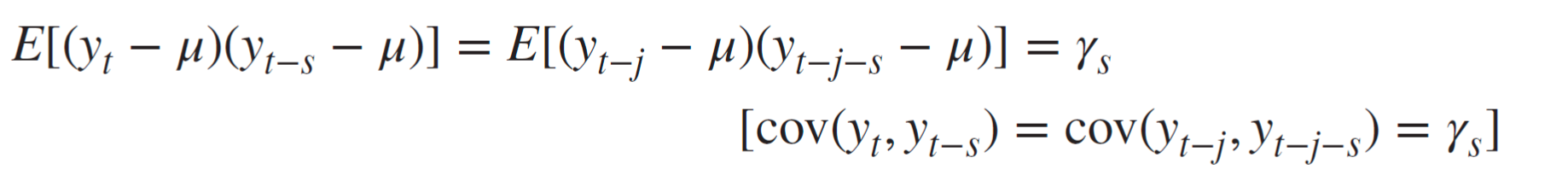
3. 현재 시점과 과거 특정시점(yt-s)의 관계식이 현재시점에서 며칠을 뺀 시점(yt-j)과 과거 특정시점에서 며칠을 뺀 시점(yt-j-s)의 관계식과 동일해야한다.
단점
1. lagging존재할 수 있음(외부의 다른 데이터를 사용해서 해결가능)
2. feature이 많을 경우 적합하지 않다. (feature 많을 경우 머신러닝 사용하기)
ARIMA
stationary(정상성)을 만족시키기 위한 차분 진행한 ARMA모형이다. 대부분 1차 혹은 2차 차분까지 진행하면 stationary한 데이터를 얻을 수 있다.
stationary데이터인지 확인하는 방법
ACF와 PACF 그래프를 사용하여 둘 중 한 그래프라도 우하향 또는 사인파를 띄는 그래프가 있다면 stationary하지 않은 데이터임을 알 수 있다.


ARIMA모형에 필요한 변수값
p: AR모형의 차수
d: 차분할 회수
q: MA모형의 차수
보통 시계열 데이터는 AR(Autoregressive) MA(Moving Average) 성질 중 하나만 가지므로 p또는 q의 값 중 하나는 0이된다.
1-1) p의 값을 가지는 경우
- ACF그래프가 우하향 또는 사인파를 띈다.
1-2) p의 값 찾는 방법
- PACF그래프에서 0으로 수렴하기 직전 lag(x값)를 찾는다. (x값이 p인 이후에 0으로 수렴한다.)
2-1) q의 값을 가지는 경우
- PACF그래프가 우하향 또는 사인파를 띈다.
2-2) q의 값 찾는 방법
- ACF그래프에서 0으로 수렴하기 직전 lag(x값)를 찾는다.
d의 값 찾는 법
- 1차 차분을 진행한 후 stationary가 만족되면 d는 1이며 2차 차분을 진행한 후에 stationary가 만족되면 d는 2이다.
'머신러닝 > 데이터분석' 카테고리의 다른 글
| z-score 기반의 이상치 제거 (0) | 2024.03.30 |
|---|---|
| IQR(사분위수) 기반 이상치 검출 및 해결방안 (0) | 2024.03.30 |
| 데이터 가공 - 데이터 증강 SMOTE (0) | 2024.03.30 |
| 데이터가공 - 문자열 변환 (0) | 2024.03.30 |
| 다중 공선성 (0) | 2024.03.30 |